Grover en acción
El problema a resolver
Vamos a resolver el problema 3SAT dado por
$\lnot \left(\lnot x \land \lnot y \right) \land \lnot y$
usando el algoritmo de Glover. Para ello necesitamos crear el Oráculo que define la acción de
las cláusulas lógicas anteriores sobre los qubits. Vamos a representar
$x$ e $y$ por los cubits q[0] y q[1] respectivamente.
El oráculo
Empecemos por ver qué hace el siguiente circuito:
cuya implementación es SAT Oracle Clause 1.
Efectivamente, este circuito hace la operación AND: $\lnot x \land \lnot y$ y si el cubit 2 está en el estado 0, se guarda el resultado de dicha operación en el mismo. Finalmente los NOT sobre los cubit 0 y 1 los devuelven a su estado original.
De la misma forma se puede seguir operando sobre los cubits, negando ahora el resultado de la operación anterior para obtener $\lnot \left(\lnot x \land \lnot y \right)$ en el cubit 3
En el siguiente paso, se realiza el último AND entre el resultado anterior y $\lnot y$.
Finalmente, es necesario deshacer las operaciones sobre los cubits auxiliares q[2] y q[3]. En efecto, como el estado cuántico está
compuesto de todas las contribuciones de los cubits, es importante
‘borrar’ el estado de esos cubits auxiliares para que solamente se tenga
como inputs los valores necesarios de los cubits 0, 1 y 4 en el siguiente
paso.

El circuito difusor
Para el difusor se propone el siguiente circuito:
que se encuentra acá.
Finalmente, el circuito completo es SAT Solver
El resultado que se obtiene al correr 1024 instancias es:
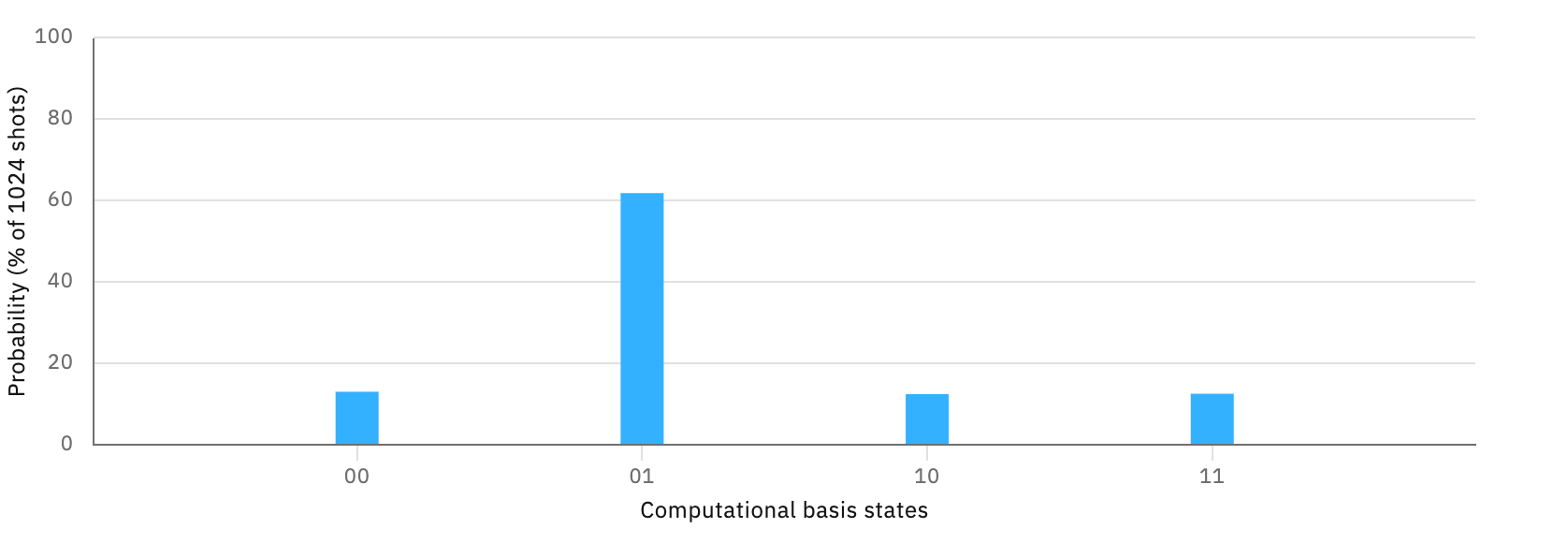
Es decir, $x=1$ y $y=0$ con alta probabilidad, que es el resultado esperado clásicamente.


